TLA+ is easy if you know how to abstract

Published on 2023-10-26 | Last update: 2024-12-05 | 13 min read

I've been wanting to learn TLA⁺ for a while now, and I finally had a chance to do it thanks to a seminar series held by Professor Murat Demirbas. In this article, I will talk about my experience with formal methods and TLA⁺, and I will also share some of the things I've learnt that I think will be very useful when writing your specifications.

By the end of this article, I hope that you will:

1. Have a basic understanding of formal methods and model checking
2. Understand how TLA⁺ can improve algorithm and system design
3. Have some intuition on what it takes to write a spec in TLA⁺
4. Want to learn some TLA⁺.

As always, let's start with the problem we're trying to solve.

What problem do formal methods help solve?

English is considered an ambiguous language, and yet we use it to write design specifications (henceforth "spec"). TLA⁺ uses math, a formal and unambiguous language, to help define a rigorous system model. After we have written the spec, we can then also use it to verify some properties.

The benefits of formal methods are twofold:

1. Unambiguous specification of our systems and algorithms
2. Verification of properties for these models

An example of a property that can be verified is that no execution can result in a deadlock. This would be very difficult to prove in a code based test, especially if it spans multiple systems.

We can also verify that an algorithm is correct by writing some properties as invariants. An invariant is simply a predicate that should always hold true. Invariants are sometimes used in code with asserts.

Any property is an intersection of correctness and liveness. For example, we could verify that eventually some property will hold, such as that our leader election algorithm eventually finishes.

Formal methods allow you to explore different designs and optimize performance while maintaining confidence that the system is doing the right thing.

Formal Methods are not a substitute to testing

Engineers tend to complain that formal methods are not useful. Their complaints typically go along the lines of:

You first spend a lot of time writing the full specification of your system, and then you spend a lot more time translating that spec to working code. Wouldn't it be easier to just have everything written as code?

There are a few fallacies in this reasoning, though:

1. It takes a lot of time to write a specification: A specification can be written in a matter of hours. See the talk by Markus A. Kuppe "Weeks of Debugging Can Save You Hours of TLA⁺". For example, to write a spec for a database, I don't need to worry about logging, efficiently handling socket connections and memory, or avoiding SEGFAULTs. In real code, I would need to take care of all of these things, but when writing a spec, these details are abstracted away.
2. A specification is a complete representation of our system: While we can certainly strive to write a full spec of our system, usually we choose to model only tricky parts of the system to verify that certain properties hold.
3. I can use that time to write the code instead: (My claim) It's not possible to write code without knowing what you are going to implement. It's similar to spending time writing a design document before diving into the code. Why do you need to spend time writing a design doc?

It is also true that, while formal methods can be used to catch bugs and debugging, they are not a substitute for testing. Formal methods help us debug our thinking about the system.

After we've written the specs, can we make sure that our implementation adheres to the spec? In the most general case, we can't. But that's ok: specs are used to debug the design.

For completeness, some formal method tools try to automatically write the system starting from a spec, or can automatically generate a test case from the stack trace of a tricky bug. However, at the time of this writing this is not available with TLA⁺.

I would also recommend reading about the usage of lightweight formal methods at AWS.

Short introduction to TLA⁺

TLA⁺ started as a formal specification language created by Leslie Lamport, a Turing Award winner and prolific contributor to concurrent and distributed systems.

The entire system is described as a state machine.

To write the specification of this state machine, we need to define:

• Some variables
• Initial state
• Some actions to go from the current state to the next

And this is enough to describe any computation!

The model checker, called TLC, navigates through all possible states and verifies the properties we defined. TLC allows us to verify two kinds of temporal properties: liveness and safety properties. Respectively, they're usually described as "something good happens" and "nothing bad happens." Invariants can be used to describe an invalid state. As soon as a safety property is violated, TLC halts and outputs the smallest "trace" of state changes that lead to the bad state.

For a banking system, I could write an invariant to check that "balance is never below zero". But if a user is never able to change the balance, the invariant is trivially true, and while in our system nothing bad happens, nothing good is happening either.

We can specify temporal properties in TLA⁺ using temporal operators. An example of temporal operators is the diamond operator <>P which says that "eventually P is true in at least one state". After we specified such temporal property, TLC will be able to verify it for us. But when this property is violated, we don't get a trace back. This is because there is no specific state that is explicitly breaking the temporal property; but the model simply failed to verify P in any state.

When the execution completes and no constraint is violated, TLA⁺ does not provide any trace—it will just say "Success". Be aware that "Success" does not necessarily imply that the model is working correctly. We will talk more about this in the bait invariants section.

Because TLC travels through all possible states, we need to try to keep the state space small. At scale, it's not uncommon to rent a high-end EC2 instance to run TLC for several hours.

It is possible to write specifications in either of two languages: TLA⁺ and PlusCal.

PlusCal is a language at a higher level than TLA⁺, and it's generally easier to follow. Resembling a common programming language, PlusCal has the advantage of being easier to read even by people without prior knowledge of TLA⁺ (or even a technical background). It's recommended for writing more sequential-style algorithms. However, TLC can only interpret TLA⁺, so after writing some PlusCal, the first step is to compile it to TLA⁺.

If we're planning to prove some properties for a spec we're writing, it might make sense to work backwards from the properties we want to prove to understand how to abstract away unnecessary details.

Why TLA⁺ is hard to learn

I've read a few articles in which people claim that TLA⁺ is hard to learn because specifications have to be written using math. However, the level of math needed is quite basic. In my experience, the hard parts of TLA⁺ are:

1. Learning how to write the specification we have in mind. This requires knowing the TLA⁺ or PlusCal language, and because the available constructs are not mapped from a programming language, it can be challenging to know where to start. Also, there are not too many resources available online.
2. Understanding the problem so well that we're able to model it. Because we're writing a rigorous specification, we're expected to understand the system we're describing very well. While writing the spec, we will find gaps in our understanding, and this is what will make writing the spec itself a useful exercise, even without the model checking part.
3. Learning how to abstract the system to its core. Professor Demirbas's opinion on abstraction:

Don't get me wrong. I found abstraction the hardest thing to teach in my series. It is almost as if it requires osmosis and some transfer of zen to communicate the abstraction idea. It still remains pretty much an art.

That post also gives an example of why learning how to abstract is important:

When we went over a two-phase commit model, they asked me why this is using shared memory rather than message passing. I explained that for the properties I like to explore, such as blocking upon transaction manager (TM) failure, the shared memory model is enough where the TM can read the states of resource managers (RMs) and RMs can read the state of TM.

Some concepts to dig more

These are few things I found useful while learning how to write TLA⁺ specs.

Read the spec as a PDF

Leslie Lamport, the inventor of TLA⁺, also invented LaTeX, a markup language for writing documents.

If you have a LaTeX compiler installed on your machine, you can compile TLA⁺ specifications to a very readable PDF format. In my experience, reading TLA⁺ as a beginner can be difficult, but reading the compiled PDF is quite helpful for understanding what is going on.

Compare the code:

\A element \in S: element # 2

with its compiled output:

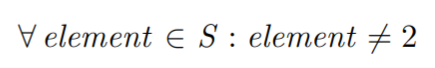
Bait invariants

Bait invariants are the equivalent of prints in programming in terms of usefulness. However, I could not find any references online about bait invariants other than Professor Demirbas's blog-I think it's safe to assume he came up with this concept.

The idea behind bait invariants is to make TLC fail on purpose. This can be thought of as a form of mutation testing.

My favorite example of a bait invariant was shared by Professor Demirbas:

baitinv ==  TLCGet("level") < 14

The TLC level is the depth during state exploration. If our maximum depth is 14, this will cause model checking to fail and TLC to print out the longest possible chain of state changes in our model. This is very useful for checking if the actual execution matches our expectations. As mentioned before, when the model checking succeeds, we only get a "Success" as output. But maybe we don't violate any invariant because a state is never reached due to a bug in the spec.

Another way to get a more specific trace would be to temporarily negate the property we are checking.

Additionally, Lamport himself recommends to "Always be suspicious of success".

Using refinements

Refinements are another interesting concept that I wasn't aware of before the seminar lessons.

We can define the spec of a problem in a very abstract way, and then use refinements to define new specs of the problem that are less abstract. We can continue writing less abstract specs until we reach the right level of abstraction for checking the properties we need.

For example, we can define a Consensus spec. We can verify generic properties of a Consensus protocol, such as the fact that some value will be eventually chosen and will never change. Then, we can write the spec for Paxos and declare that Paxos refines Consensus. In the Paxos spec, we can verify additional properties specific to this algorithm that should hold true.

This helps us ensure that we are looking at the problem at the right level of abstraction. More succinctly:

Refinement mappings are used to prove that a lower-level specification correctly implements a higher-level one. The Existence of Refinement Mappings

This is explained very well in this video: "The Paxos algorithm or how to win a Turing Award" by Leslie Lamport.

Weak/Strong fairness

This is an advanced concept, but it is good to be at least aware of it. After publishing, I've updated on this section as recommended by Professor Michel Charpentier, for which I am truly grateful.

An unfair system is one that if it can diverge into the same loop and never make any progress, it will do so. It means that when we're computing the next state, if it is possible to stay in the same state, the system will choose that state change and will simply stop making progress. This will break liveness properties.

If the process you're modeling is not "unfair", you can declare the available set of actions as weakly fair. A weakly fair system ensures that if we have a state change that would lead to making progress, this state change will be taken at least once.

On Weak fairness, Professor Charpentier says that is important and is necessary to model the individual progress of processes. At its simplest, it's just a way to ensure that "code" does not stop between instructions for no particular reason.

Other than weak fairness, we also have strong fairness, which guarantees that if an action is not permanently disabled, it will eventually be taken.

On Strong fairness, Professor Charpentier says that Strong fairness makes sense in the context of refinement, as something that will need to be refined into a weak fairness only protocol before it can be implemented. I feel that it can be safely ignored outside refinement proofs.

I have found these concepts useful when I wanted to write a spec that included a retry mechanism. I recommend reading Strong and weak fairness by Hillel Wayne to learn more.

How to get started with TLA⁺?

My suggestion would be to install the TLA⁺ extension on VS Code and interact with TLC from there. The extension is everything you need to get up and running, apart from java 10.

If you're curious to learn more about TLA⁺, I've added some additional resources below. As a next step, I would definitely recommend watching part 1 and 2 of The Paxos algorithm or how to win a Turing Award by Leslie Lamport. It goes into details on everything I've covered here and gives a crash course on TLA⁺. After that, your next stop is probably Specifying Systems book by Leslie Lamport.

Conclusion

TLA⁺ is a formal specification language created by Leslie Lamport. TLC is a tool that uses TLA⁺ specs for model checking. Learning TLA⁺ is challenging because we need to understand a problem well enough to be able to write its specification, know the TLA⁺'s language, and abstract the problem effectively.

If you also believe that writing helps with reasoning, then TLA⁺ is the tool for you. Writing the spec helps to find gaps in your understanding, and a spec can help debug your design. However, a TLA⁺ spec is not a substitute for testing.

In my next post, I will present an example of a simple-to-understand problem to demonstrate how difficult it can be to abstract correctly, even if you understand the problem and the TLA⁺ constructs needed to represent it.

This post concluded with some (I hope) interesting TLA⁺ notions: bait invariants, as useful as println in programming; refinements, abstraction in inheritance style; weak/strong fairness, to help model the behavior of real systems.

I hope you enjoyed reading this article and that it has made you curious enough to learn some TLA⁺ this weekend.

I'm planning to write more posts about TLA⁺, so follow me on Mastodon or Twitter if you don't want to miss them!

Acknowledgments

I would like to thank Maria Giulia Cecchini for reviewing the draft for this article - of course, the errors and mistakes are still mine.

Professor Michel Charpentier provided very good feedback on the article, pointing out few mistakes I had amended and reported in the Edits section.

I really owe a lot to Professor Demirbas and his seminars, they really helped me getting started on TLA⁺.

Resources and References

As promised, some resources I can recommend:

• Specifying systems book by Leslie Lamport.
• TLA⁺ Video Course by Leslie Lamport.
• PlusCal c-style manual https://lamport.azurewebsites.net/tla/c-manual.pdf
• Professor Demirbas has written a lot on TLA⁺, so a simple search will yield many articles.
• https://learntla.com/index.html has a lot of documentation.
• Beyond the Code: TLA⁺ and the Art of Abstraction by Professor Murat Demirbas. Talks about the experience of teaching TLA⁺ at the seminars. I guess it can be considered the view from "the other side" of this post.
• Teaching Concurrency by Leslie Lamport. Lamport's take on what engineers should learn about concurrency.
• Strong and weak fairness by Hillel Wayne.
• Using lightweight formal methods to validate a key-value storage node in Amazon S3.
• Use of Formal Methods at Amazon Web Services by Newcombe et al.
• TLA⁺ Example repo has lots of examples, though not many are written in PlusCal: https://github.com/tlaplus/Examples.

Revisions

2023-11-30: I made a few edits after some very thorough review from Professor Michel Charpentier on LinkedIn:

• When presenting TLA⁺, I mistakenly called TLA⁺ a model checking tool; but TLC is the model checking and TLA⁺ is a specification language. TLC, the tool used for model checking, was created a long time after it. Professor Demirbas mentioned this a few times, but I still managed to write it wrong.
• In the introduction to TLA⁺ section, I neglected to mention that you don't get counterexamples for invalided temporal properties, but only for invariant-based properties. I've rephrased the relevant section and used the diamond operator as an example.
• In the "Read the spec as a PDF" section, my LaTeX example may look a bit silly, but I did not change it because the point is just to let the novice user be aware of this useful feature.
• I've shrunken the Weak/Strong fairness section. I've reworded it a little bit and included some wisdom by Professor Charpentier. I've also decided to remove the example as, after the reviewing recommended by his comment, I think it was not helping clear these concepts. The linked article in that section has a more in-depth explanation and will be more helpful. 2024-12-05: Updated few bits here and there, now that I have more experience with TLA⁺.
• Replaced TLA+ -> TLA⁺
• In "Using Refinments" section, I'm now using Consensus as an example instead of sorting. It's also the same example provided by Lamport in the attached video, so I think it makes more sense this way.