Federico Ponzi's Blog

Home Blog SWAG

Wolf, goat and cabbage problem TLA+ modeling

Published on 2023-10-30 | Last update: 2024-10-29 | 12 min read

Table of Contents

In this article, I'm going to share my modeling process to the Wolf, goat and cabbage problem in TLA+.

As explained in my previous article, TLA+ is a model checking tool that allows you to model a complex system and prove some properties on it.

The idea is to:

  1. Model the problem in TLA+ - I've used PlusCal.
  2. Write a property that describes the solution.
  3. Negate the above property.

Because TLA+ works by exploring the full state space, if there is a state that satisfies the property for the solution to the problem, TLC will show us the minimum number of state changes needed to get there.

I will first quickly show you how to set up your development environment, then walk through my modeling process, and finally I'll describe the code for the solution. Along the way, I will also talk about the TLA+/PlusCal constructs I've used.

I hope that by reading this article you will:

Setting up the environment

There are two options here.

The first option would be to use the TLA+ toolbox, an Eclipse-like IDE. You can download it from the official website.

The other option, which I recommend, is using Visual Studio Code and installing the TLA+ plugin. There are two plugin versions; at the time of this writing, I would recommend getting the nightly version as I found bugs in the "stable" version. Also, the nightly has more features.

A TLA+ specification is a my_spec.tla containing your TLA+ code along with a config my_spec.cfg file. You can type ctrl+shift+p to open VsCode command palette. Then you can use TLA+: Parse module to translate your PlusCal to TLA+ and TLA+: Check model with TLC to run TLC.

Wolf, goat and cabbage

TLA+ is often presented by modeling a very complex algorithm. If you remember the three reasons I've identified on why TLA+ is hard to learn in my previous article, one of them was about understanding the problem we're trying to model.

The problem recites:

A farmer with a wolf, a goat, and a cabbage must cross a river by boat. The boat can carry only the farmer and a single item. If left unattended together, the wolf would eat the goat, or the goat would eat the cabbage. How can they cross the river without anything being eaten? https://en.wikipedia.org/wiki/Wolf,_goat_and_cabbage_problem

This problem is easy enough that you can understand it and solve it in a few minutes. So now we're left with the other two problems: understanding how to represent it in TLA+ language and how to correctly abstract it.

I've found this exercise on Professor Demirbas's blog, in which he also explains how he solved it.

I will first describe my idea for the solution. Then I will walk through the Pluscal code. Before moving forward, try to solve it in your head, and when you're ready, keep on reading.

First iteration

I started by thinking about states. What changes as the system evolves? We have two sides of the river that will hold different "items" (I decided to use items to refer to Wolf, Cabbage and Goat). The "transport" (the boat) also can be holding one of these items at any time. So we have a transport, an end side and a start side.

Then I needed to think about initial states and next actions.

For initial states, end side is empty because everything is on the start side. Transport is also empty.

For the next actions:

Now for the second action, we have a problem: we cannot leave say Cabbage to the same side of the Goat otherwise it would not end up well. So if by leaving the item to the side we reach an unsafe state, we should pick another item from the same side — essentially swapping the items.

In my initial attempt, I tried modeling 4 actions, 2 per side:

I implemented this (you can check the git history for the code) and was correct. But it was more complicated than necessary because of the swapping.

I already have action 1 to pick an item from either side. Therefore, the second action could have been simplified to only drop item from transport.

Second iteration

The second iteration tried to simplify the above. The drop item from transport action is super simple: if the transport is loaded, choose either side and drop the item.

Then to decide if we can pick an item from a side, I added a guard that ensures we cannot pick an item from a side if the other is in an unsafe state. This is to force to pick an item from the unsafe side. If both sides are in a safe state, we can choose to pick from either of them.

And this is enough to model all the rules of our problem!

Wait, why aren't we talking about the solution?

This model allows silly movements like:

  1. load goat from side start,
  2. unloading it to side start.

But that's completely fine. TLC will go through all the possible states and try to verify that the invariant we defined hold. In this case, I've decided to write the invariant by stating that "(it is impossible to) ever end up in a state in which all items are on the end side of the beach."

I hope it is clear that this exercise is about modeling the problem/system. TLC will provide the solution to us.

My first iteration was also too much focused on trying to model the solution. But the model should stay objective, and it should not put unneeded constraints.

Pluscal code

Let's start writing the PlusCal code for the solution. You can get the full tla spec and cfg file from GitHub.

As a start, we need to define the header:

Everything written here is ignored.
---- MODULE wolf_goat_cabbage ----

This is normal TLA+ code.

Then we need to import the definitions for TLC, FiniteSets, and Integers.

\* Used by bait invariant
LOCAL INSTANCE TLC
LOCAL INSTANCE Integers
\* Used by the spec.
LOCAL INSTANCE FiniteSets

LOCAL INSTANCE allows you to import definitions without re-exporting them. Alternatively, people tend to use EXTENDS for imports. Check out the docs here.

Some definition follows:

WOLF == "Wolf"
GOAT == "Goat"
CABBAGE == "Cabbage"
All == {WOLF, GOAT, CABBAGE}
InvalidStates == {{CABBAGE, GOAT}, {WOLF, GOAT}}
baitinv == TRUE
\*baitinv ==  TLCGet("level") < 14

This is normal TLA+ code.

== is used for equality, and it reads as "is by definition". It can be thought as an assignment.

All defines a set that will be later used to verify that everyone got to the end side.

These definitions are like constants at the top of my spec. But constants can also be defined in the config file and instantiated here. Using the .cfg file is usually the best practice.

baitinv is a special invariant I use for debugging called Bait Invariant. When TLC explores the state space, it will do a graph visit and TLCGet("level") returns the current level of depth. If it's greater or equal than 14, TLC will stop and report a stack trace. I touched on this in the previous article about TLA+.

I defined baitinv as an invariant inside the cfg file. I keep both of them because when I don't need to debug, I will toggle the comment between the two lines.

Let's start with the Pluscal part. Pluscal code is included as a TLA+ block comment, so in between (* and *).

(*--algorithm wolf_goat_cabbage {

variables side_start = All, side_end = {};

define {
    IsValidState(side) == ~(side \in InvalidStates)
    Invariant == side_end # All
    \* this operator is used select an item
    \* from side such that removing this item
    \* will leave "side" in a valid state.
    ValidSubsets(side) == {s \in SUBSET(side): IsValidState(side_start \ s) /\ Cardinality(s) = 1}
}

algorithm is used to start the Pluscal code. The name is arbitrary.

Variables are global in our algorithm.

The define block allow us to write operators and definitions that refer to the global variables.

The # character is used to denote inequality (your != in programming languages) and SetA \ SetB is used to compute the difference between the first and the second set.

macro PickFrom(side, other_side_is_valid) {
    await /\ transport = {} 
          /\ side # {} /\ other_side_is_valid;
    \* choose an item such that this side is left valid:
    with( item \in ValidSubsets(side)) {
        transport := item;
        side := side \ transport;
    }
}

macro DropItemTo(side) {
    \* leave an item to side_start side. If needed to avoid conflicts, load the other item.
    await transport # {};
    side := side \union transport;
    transport := {};
}

macro can be used to write macros. These code blocks syntactically replace the code where the macro is invoked. So in there, we can refer to local variables (like transport) even if they're not defined locally.

PickFrom and DropItemTo are macros that contain the code to respectively pick from a side and drop to a side.

await is our guard condition. It prevents this action from being picked, unless the guard condition is true. If you're familiar with match/case in functional programming languages like Scala or Rust, it works in the same way.

The syntax for chaining multiple conditions is a bit unusual, but Lamport explains in this video that mathematicians don't need to write such long and complicated and/or chains, and this syntax scales well. In this case, the interline alignment has semantic meaning.

The := is for assigning a state to the variable. It's the = in your usual programming language. But in TLA+, "=" stands for equality. So saying "transport = {}" is a predicate for checking that "transport is empty".

PickFrom takes an other_side_is_valid variable to make it nicer to read from the caller side. As we mentioned before, we should pick from this side only if the other side is in a safe state.

with is used to insert randomness. Initially I used the CHOOSE operator, but then I figured out that it's not what I needed. CHOOSE should rather be thought as "always pick the least item in the set of items that verify a predicate":

What if multiple values satisfy CHOOSE? In this case the only requirement is that the result is deterministic: the engine must always return the same value, no matter what. In practice this means that TLC will always choose the lowest value that matches the set. https://learntla.com/core/operators.html#choose

with will do the right thing, and pick a random item from the set.

We're ready to check the main section of the algorithm:

process (Farmer = 1) 
variable transport = {}; {
W:
    while (TRUE){
        either {
            \* pick an item from side_start and load it.
            PickFrom(side_start, IsValidState(side_end));
        } or {
            \* pick an item from side_start and load it.
            PickFrom(side_end, IsValidState(side_start));
        } or {
            DropItemTo(side_start);
        } or {
            DropItemTo(side_end);
        };
    }
}
}*) \* this closes the comment at the start of the algorithm: (* --algorithm

We define a new process—a single process called Farmer - which has a local variable called transport.

In a loop, it tries to load something or drop the item somewhere. And that's it!

Using the TLA+ plugin, we can use "TLA+: Parse module" to generate the TLA+ code from the Pluscal.

After the line \* END TRANSLATION you can add more code that won't be overwritten on the next call of Parse Module. I've added my TypeOk definition here:

\* END TRANSLATION 

TypeOk == /\ \A el \in side_start : el \in All
          /\ \A el \in side_end : el \in All
          /\ \A el \in transport : el \in All
====
All specs conclude with a number of "===". Everything written after (like this text) is ignored by TLC.

Because TLA+ is not type-checked, we can end up in a situation in which we assign something by mistake to a variable. TypeOk is the usual way to enforce some type checking, and yes, it's just another invariant.

We can define the config file wolf_cabbage_goat.cfg (the name has to match the .tla file):

SPECIFICATION Spec
\* Add statements after this line.
INVARIANT  
    Invariant
    TypeOk
    baitinv

CHECK_DEADLOCK
    TRUE

and now we can call "TLA+: Check module with TLC" to run the model checker:

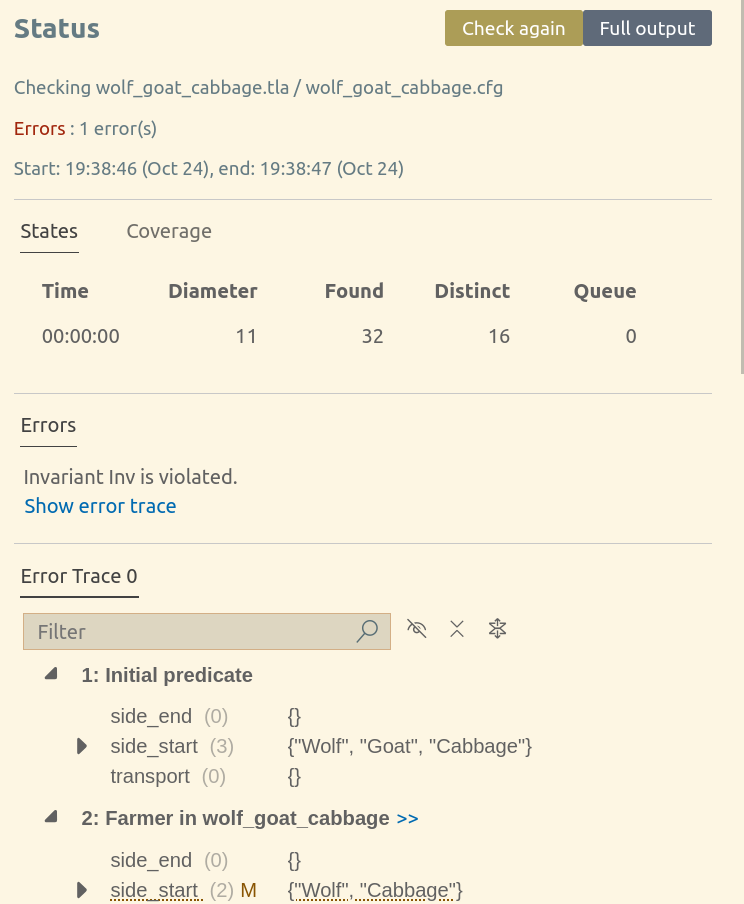
tlc-output-1

tlc-output-2

tlc-output-3

So the steps are:

  1. load goat
  2. unload goat to the end side
  3. load wolf
  4. unload wolf to the end side
  5. load goat
  6. unload goat to side start
  7. load cabbage
  8. unload cabbage to the end side
  9. load goat
  10. unload goat to the end side

All the items end up in the end side and the invariant inv is violated. TLC produced a counter-proof by showing us the minimum state changes required to get there, exactly as we expected!

Can we do better?

My TLA+ spec was written from the perspective of the transport. But we could potentially think about the two sides as nodes and transport as their communication channel. This is what professor Demirbas has modeled in his solution.

But do we even need a transport or is it an unnecessary detail? In this description of a solution, we never really had to mention the transport at all:

  1. move goat to the end side
  2. move wolf to the end side
  3. move goat to the start side
  4. move cabbage to the end side
  5. move goat to the end side

And this is what Professor Michel Charpentier modeled in his solution. It is available on Professor Demirbas's blog, but I've reproduced it here for your convenience:

------- MODULE wcg ----
EXTENDS FiniteSets
CONSTANT Goat, Cabbage, Wolf, Man

All == {Goat, Cabbage, Wolf, Man}
ASSUME Cardinality(All) = 4
VARIABLES L
Init == L = All 
R == All \ L

Safe(s) == /\ {Goat, Cabbage} \subseteq s => Man \in s
           /\ {Goat, Wolf } \subseteq s => Man \in s

TypeInv == L \subseteq All /\ Safe(L) /\ Safe(R)

Move(x) == /\ \/ /\ {x, Man} \subseteq L
                 /\ L' = L \ {x, Man}
              \/ /\ {x, Man} \subseteq R
                 /\ L' = L \union {x, Man}
           /\ Safe(L')
           /\ Safe(R')

Next == \E x \in All : Move(x)

Prog == Init /\ [][Next]_L
Impossible == [](R # All)

====

wcg.cfg file:

CONSTANTS 
    Goat = Goat
    Cabbage = Cabbage
    Wolf = Wolf
    Man = Man

SPECIFICATION 
    Prog

INVARIANTS 
    TypeInv

PROPERTIES 
    Impossible

I was very impressed by the definition of R (right side of the beach) as ALL \ L, where \ is used to compute the difference between the first and the second set.

You can also notice that the solution is much more succinct and uses TLA+ rather than PlusCal.

I think both Professors' solutions are interesting. They modeled the problem from the river's point of view. In their models, a beach is a process, while in my model the farmer is a process. Their solution allows to potentially scale the solution with respect to the number of beaches.

Conclusions

In this article, I've explored my design process and my solution of the Wolf, goat and cabbage problem. I've also explained the TLA+ constructs I've used as I was presenting them because even if TLA+ is a very nice tool, in my opinion, there are not enough resources online explaining how to use it.

Working on this problem was a very nice exercise, I've been wanting to solve it since Professor Demirbas mentioned it. While it doesn't require extensive knowledge of TLA+, and the problem is easy to understand, getting the modeling right requires some thinking.

If you already know some TLA+, I would recommend trying solving this exercise. You can then compare your solution with the one in Professor Demirbas's blog, or with mine. If you need some more inspiration, you can try solving the tower of hanoi or the Die Hard exercise proposed by Leslie Lamport in his video tutorial about TLA+. If you want to try something more advanced, you can browse the TLA+ Examples repo and try to contribute some missing spec or propose alternative modelings in PlusCal.

References